K-nearnest neighbor #

Concept #

KNN is a special case where no learning is performed. It is a supervised machine learning algorithm. It is also a non-parametric algorithm, meaning it does not have strict requirements for the underlying distribution of the data. It can be used for regression or classification. The data points are grouped together baesd on similarity metric. The prediction is baed on training data only. sklearn implementation of KNeighbors can be found here.

Algorithm #

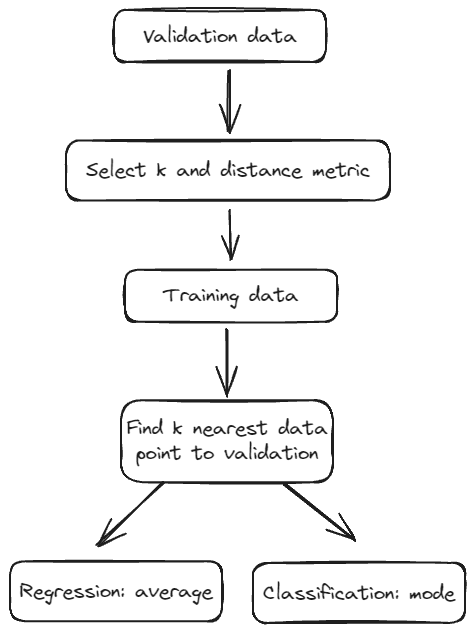
• Split into training and validation set.
• Normalize data
• For each validation data point, estimate its distance to all data in training
• Select first k data points in training closest to the validation data point, using the distance metric
• Regression uses k-nearest neighbors’ mean to predict
• Classification uses majority voting decide the prediction, if there is a tie then tie-breaking mechanism is required

Distance calculation methods #

• Euclidean
  • straight line distance
  • supports the standard concept of spatial distance
  • this distance is known as the l2-norm
• Hamming distance
  • number of positions at which corresponding symbols are different for two strings.
  • used for comparision of binary data strings
• Haversine
  • calculates the distance travelled over the surface of a sphere, such as the Earth
• Chebychev
  • assumes the distance is equal to the greatest distance along the individual dimensions
• Minkowski
  • a generalization of the Manhattan and Euclidean distances to arbitrary powers
  • suitable when there’s correlation between features, p=1 is just manhattan distance and p=2 is just euclidean
• Manhattan
  • restricts distance measurements to follow grid lines.
  • this is sometimes referred to as the Taxi cab distance, since taxis must follow streets, which also gives rise to its formal name, manhattan, for the street grid on the island of Manhattan.
  • this distance is also known as the l1-norm
• Mahalanobis
  • measure of the distance between a point and a distribution, considering the correlations between features.
• Cosine
  • calculate similiarity between vectors
  • cosine angle of the bectors
• Jaccard
  • similar to cosine

How is K selected #

This requires testing and identify the use case of the model. It can be found by experimenting with various k values and check the error rate. At a certain point the accuracy improvement will no longer be significant. The rule of thumb is to use k=sqrt(sample size)/2.

KNN pros and cons #

Pro：

• Easy to use, no actual “parameter tuning” required like other models
• Can be used for regression/classification

Con：

• Resource intensive when data scales up

Common use cases #

• Missing value imputation, this can be added to scikit-learn pipeline
• Quick fix for anomly detection where data can be imputated

Python implementation (sklearn) #

import numpy as np
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error
from math import sqrt
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split
(
X,
y, 
test_size=0.2,
random_state=12345
)
knn_model = KNeighborsRegressor(n_neighbors=3)
knn_model.fit(X_train, y_train)

train_preds = knn_model.predict(X_train)
mse = mean_squared_error(y_train, train_preds)
rmse = sqrt(mse)

test_preds = knn_model.predict(X_test)
mse = mean_squared_error(y_test, test_preds)
rmse = sqrt(mse)
rmse

Python implementation (raw) #

Step 1: Calculate the distance #

import numpy as np

def distance_calculation(point1,point2):
    """
    Calculates the distance between two points
    """
    distance = np.sqrt(np.sum((p1-p2)**2))
    
    return distance

Step 2: Calculate KNN #

import numpy as np

def distance_calculation(point1,point2):
    """
    Calculates the distance between two points
    """
    distance = np.sqrt(np.sum((p1-p2)**2))
    
    return distance